r là gì trong đường tròn? Tìm hiểu về khái niệm r và vai trò của nó
Gia Sư Tài Năng xin chia sẻ bài viết chi tiết về khái niệm r là gì trong đường tròn. Hãy cùng tìm hiểu về ý nghĩa và ứng dụng của r trong bài viết dưới đây!
Định nghĩa r là gì trong đường tròn
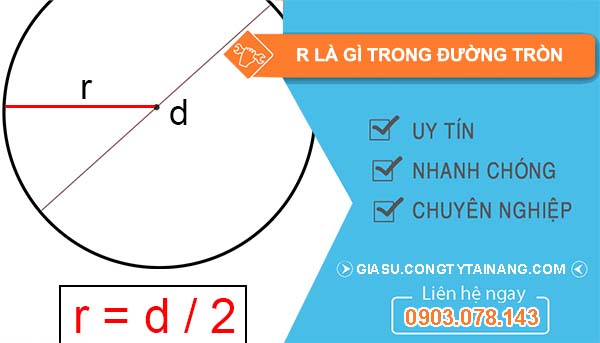
r là gì trong đường tròn? Bán kính (ký hiệu là “r”) là đoạn thẳng nối từ tâm của đường tròn đến bất kỳ điểm nào trên đường tròn đó. Tâm của đường tròn là điểm ở trung tâm của nó, là điểm cách đều mọi điểm trên đường tròn. Vì mọi điểm trên đường tròn đều có khoảng cách từ tâm giống nhau, nên bán kính của đường tròn là một đại lượng cố định.
Ví dụ, nếu một đường tròn có bán kính là 5 cm, thì mọi điểm trên đường tròn sẽ cách tâm của nó một khoảng cách là 5 cm.
Công thức tính diện tích của đường tròn
Một trong những ứng dụng quan trọng của bán kính trong đường tròn là việc tính toán diện tích của đường tròn. Diện tích của một đường tròn có thể được tính bằng công thức:
A=πr2
Trong đó:
- A là diện tích của đường tròn,
- r là bán kính của đường tròn,
- π là hằng số Pi, có giá trị xấp xỉ 3.14159.
Ví dụ, nếu bán kính của một đường tròn là 3 cm, diện tích của đường tròn sẽ là:A=π×32=π×9≈28.27 cm.
Tính chất của bán kính trong các bài toán hình học
Bán kính của đường tròn đóng vai trò quan trọng trong nhiều bài toán hình học, không chỉ trong việc tính diện tích và chu vi, mà còn trong các bài toán liên quan đến tiếp tuyến, các đường chéo, góc và các hình học liên quan khác. Dưới đây là một số tính chất quan trọng liên quan đến bán kính trong hình học:
a. Bán kính vuông góc với tiếp tuyến
Một trong những tính chất quan trọng của bán kính là: bán kính vẽ từ một điểm trên đường tròn đến tiếp tuyến của đường tròn tại điểm tiếp xúc sẽ vuông góc với tiếp tuyến. Điều này có nghĩa là nếu có một tiếp tuyến tại điểm P của đường tròn, thì bán kính nối từ tâm O đến điểm P sẽ vuông góc với tiếp tuyến tại P.
b. Bán kính chia đường tròn thành các cung
Bán kính cũng có thể chia đường tròn thành các cung. Trong hình học, một cung là một phần của đường tròn, được xác định bởi hai điểm trên đường tròn. Khi một bán kính đi qua một điểm trên đường tròn, nó chia đường tròn thành hai cung đối xứng nhau.
c. Tính chất về khoảng cách từ điểm đến đường tròn
Bán kính cũng giúp xác định các khoảng cách từ một điểm ngoài đường tròn đến đường tròn. Khoảng cách từ điểm ngoài đường tròn đến đường tròn chính là chiều dài của đoạn thẳng nối từ điểm đó đến điểm tiếp xúc của tiếp tuyến với đường tròn. Khi đoạn thẳng này có độ dài bằng bán kính của đường tròn, điểm đó sẽ trở thành một điểm tiếp xúc của tiếp tuyến với đường tròn.
Bán kính trong các dạng bài toán phức tạp
Bán kính không chỉ được sử dụng trong các bài toán cơ bản về diện tích và chu vi, mà còn là yếu tố quan trọng trong các bài toán phức tạp hơn, chẳng hạn như:
- Bài toán về các hình chóp và hình nón: Trong các bài toán về các hình chóp, hình nón hay các hình khối có cấu trúc dạng tròn, bán kính sẽ được sử dụng để tính toán thể tích, diện tích bề mặt và các yếu tố khác.
- Bài toán liên quan đến các hình học phẳng: Trong các bài toán tìm giao điểm giữa các đường tròn hoặc tiếp tuyến với đường tròn, bán kính đóng vai trò quan trọng trong việc xác định các giá trị cần thiết.
Kết luận
Bán kính là một khái niệm cơ bản và quan trọng trong hình học, đặc biệt là trong việc nghiên cứu và tính toán các yếu tố của đường tròn. Nó không chỉ giúp xác định diện tích và chu vi của đường tròn, mà còn có vai trò quan trọng trong các bài toán hình học phức tạp và các ứng dụng thực tế.
Đây là bài viết chia sẻ về khái niệm r là gì trong đường tròn của Gia Sư Tài Năng. Với mong muốn mang đến những kiến thức cơ bản và bổ ích, bài viết giúp bạn hiểu rõ hơn về bán kính của đường tròn – yếu tố quan trọng trong hình học. Hy vọng rằng những thông tin trong bài sẽ hỗ trợ bạn trong việc nắm bắt và áp dụng các công thức liên quan đến đường tròn, từ đó giải quyết tốt các bài toán hình học cũng như các ứng dụng thực tế.